Gravity
from a new angle
In Newtonian principle, force of
gravity was proposed as inversely proportional to the square of the
distance between the objects. If we double the distance between the
objects, the strength of gravity will diminish to a one fourth of the
original force between them.
A common
example we find for the derivation of this principle is how
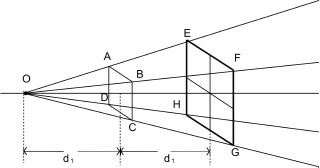
Figure 1: Inverse Square Law
the intensity of light is diminished
with the increase in distance between the light emitting point and an
object with an area as shown in Fig 1.
O is the light emitting point
and ABCD
is a square object.
The point O
and the ABCD
are separated by a distance of d1.
If the square was moved away from O
for a distance equal to d1,
the luminosity of O
on the square at new location will decrease to one fourth of the
initial.
Gravity was also assumed to work in
similar to the luminosity of a light source. In the previous example,
O is a light emitting object and
the square is a non-luminous object. Both are dissimilar objects by
nature, means one emits the light and the other doesn't. In the case of
gravity, both are mutually attracting objects. If the sun exerts
gravity on the earth then the earth also exerts gravity on the sun. If
we compare the gravity of an object with a light emitting from an
object then both the sun and the earth should be treated as light
emitting sources when calculating the gravity between them.
Another assumption made when deriving
the inverse square law for gravity, apart from assuming that gravity is
light, is that the light source was treated as a point. In reality,
wherever we study the gravity between objects, none of them were of
point mass objects. Consider the example of light reaching the Mercury
from the sun as shown in Fig 2.
O
and S
are two different points on the surface of the sun and the
d is the distance between the
sun and the Mercury from point O.
The distance between the sun and the Mercury from point
S is
x. If we double the distance of
the Mercury from the sun from point
O, the light reaching the
Mercury from the sun wouldn't be 1/4th
of the original, it will be slightly more than a quarter because the
sun is emitting the light
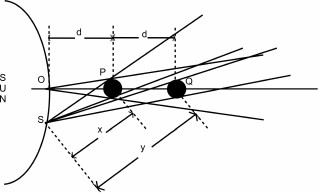
Figure 2: Relevance of Inverse square law for the distance between Sun
and Mercury.
in a wide angle instead of as a point.
Even the new position of the Mercury wouldn't be exactly double from
all other points on the sun. When the new position of the Mercury
viewed from point S,
the new distance y
is not double the distance of the earlier distance of
x. Therefore more light reaches
the Mercury than 1/4th
of the original.
As seen earlier in the chapter on mass,
an object and its point mass counterpart are not same. When a bigger
object turns to a point mass object, the new point mass object weighs
more. According to the present definition of mass, the new point mass
object gains more mass. Therefore, any principle derived assuming these
two objects are same is invalid.
Gravity is not a thing that emanates
all around an object like the light emanating from a light source.
Light source emanates the light without any external influence. Gravity
is a mutual entity. It will be felt on an object only when there is
another object in its vicinity. If there is only one object, there
wouldn't be any effect of gravity around it.
We see the waves in the ocean generated
by the gravity between the earth and the moon travelling all around the
earth due to the rotation of the earth and the revolution of the moon
around the earth. If the earth and the moon remains stationary at a
distance then the waves in the ocean always point towards the direction
of the moon.
Another aspect which inverse square law
ignored is the differential force of an object like planet Jupiter.
Bigger objects will have both resultant and differential forces. A
point size object will have only the resultant force. The effect of
differential force is missing in the point mass object.
Gravity doesn't act like the light and
the objects gravitationally interacting are not point mass objects.
Therefore the inverse square law principle, which was derived based on
the characteristics of the light emanating from a point source,
wouldn't be valid for the gravity.
The Inverse square law principle is
widely applied in physics in the derivation of the strength of light,
sound, electricity and magnetism at a new location away from the
source. It is valid for the propagation of light and sound but not for
the gravity. Inverse square law is valid for the scenarios where the
strength of a force acts all around the object irrespective of
existence of another object around it.
Date posted: October 1, 2009
Copyright
2009 Karunakar Marasakatla

